物理信息神经网络（Physics-Informed Neural Networks, PINN）通过将偏微分方程作为软约束嵌入损失函数，有效融合了物理先验与观测数据，为复杂动力系统的建模与反演提供了新兴范式。该方法在材料科学、生物医学、流体力学、传热学和生物力学等众多科学与工程领域展现出广阔前景。然而，传统PINN方法采用基于孤立配点的逐点残差损失函数进行构造，存在显著的优化冲突问题：（一）数据驱动目标与物理守恒目标之间互相竞争，存在目标冲突；（二）大量配点间的物理残差缺乏空间关联性与守恒一致性，存在空间冲突（图1）。这些冲突导致了训练过程不稳定、收敛性差等一系列问题，并显著限制其在强非线性、强耦合性问题中的预测精度与可靠性。

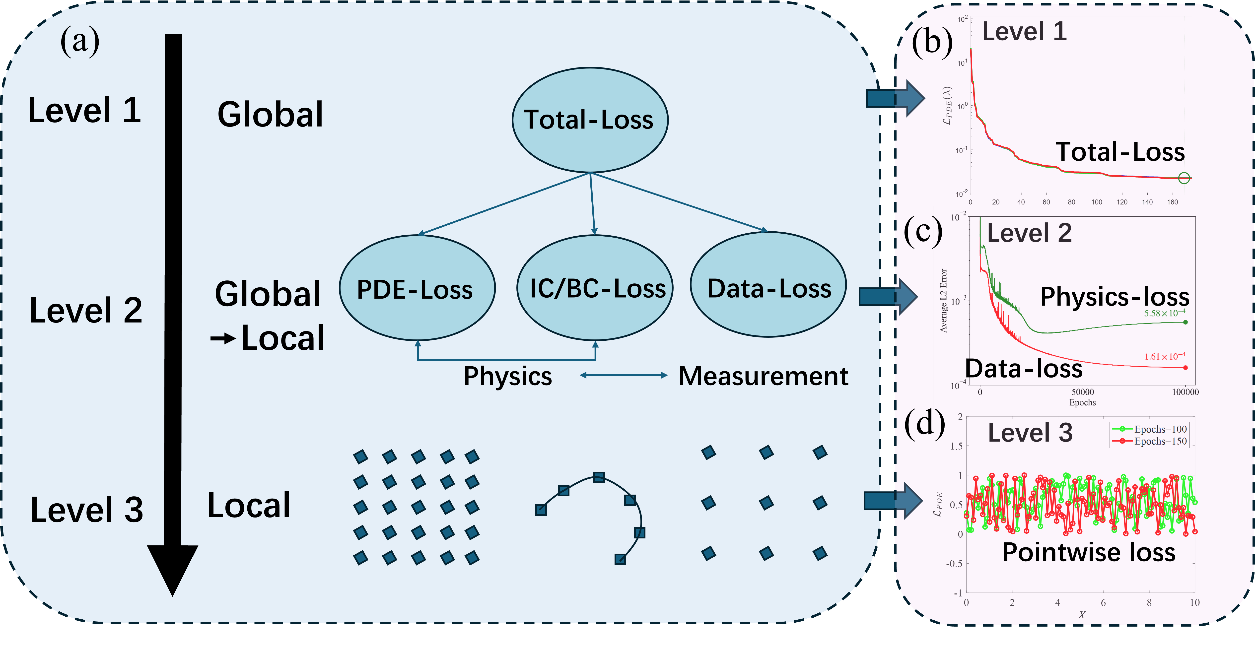
图1：PINN多层协同优化过程中的冲突问题示意图

针对上述瓶颈问题，北京大学力学与工程科学学院刘谋斌教授与钱志浩副研究员团队（先进计算与多介质耦合力学实验室）在传统PINN方法基础上，创新性地引入局域积分策略，通过在配点邻域构造守恒子域，并基于子域内质量、动量等物理量的积分残差构建全局损失函数，显著改善了多目标优化中的目标冲突与空间冲突问题。基于这一策略，团队提出了稳定化物理信息神经网络（Stabilized PINN, S-PINN）新框架，大幅度提升了训练稳定性与物理一致性。该框架兼具无网格离散的灵活性与物理守恒性，显著增强了复杂工况下的数值鲁棒性。

该团队通过压力泊松方程、Burgers方程、三维热传导、三维方腔驱动流及圆柱绕流等一系列经典基准算例，系统验证了S-PINN方法的有效性。结果表明，S-PINN不仅在预测精度上优于传统PINN，在物理量的局部与全局守恒性方面也表现出显著优势（图2–图4）。相比能量型EB-PINN方法，S-PINN在收敛效率与数值稳定性方面均具备突出优势，展现出其在科学与工程计算领域的广泛应用潜力。相关研究成果已发表于计算力学领域顶级期刊《Computer Methods in Applied Mechanics and Engineering》。

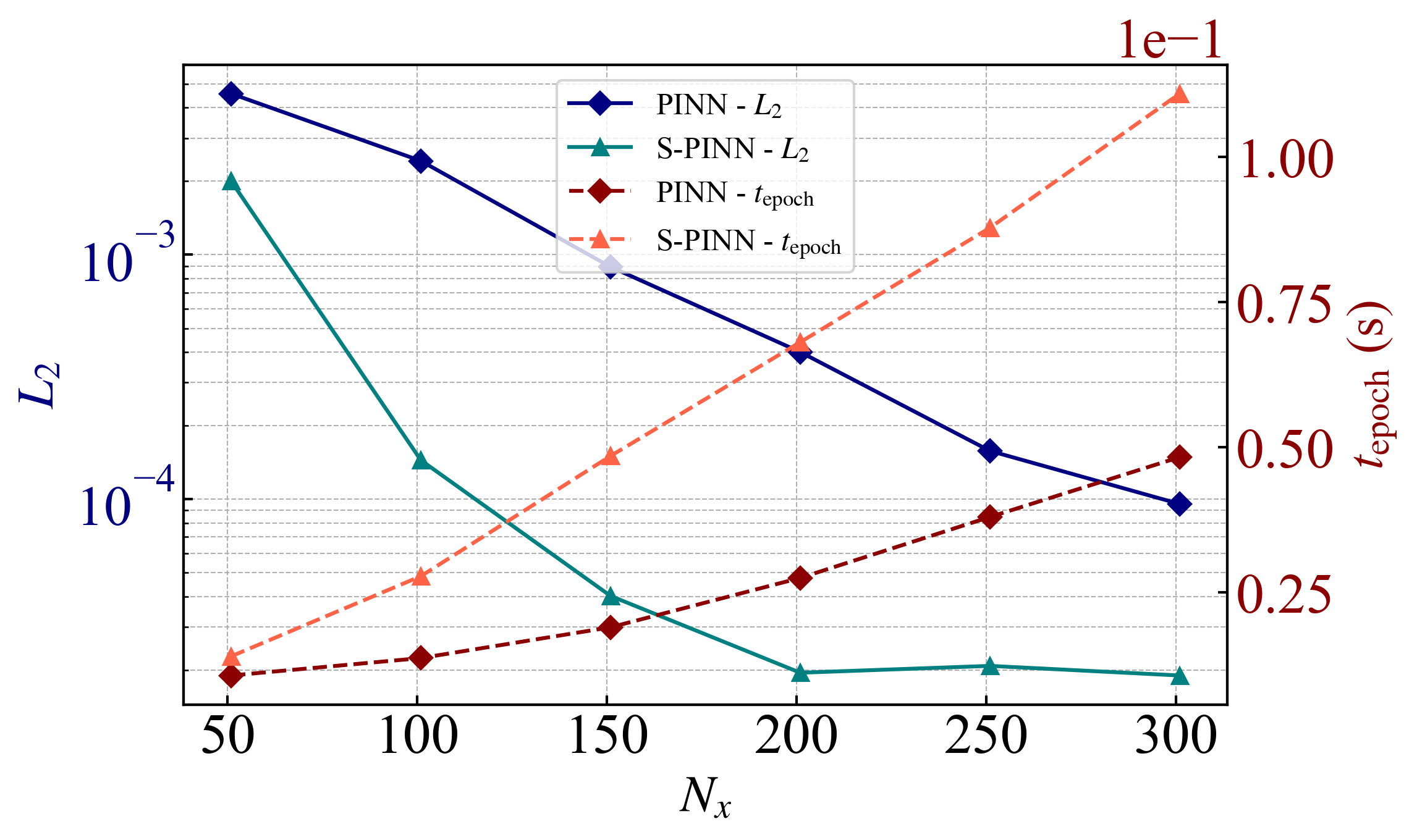
图2： Burgers方程中PINN与S-PINN的精度与效率随离散程度的变化

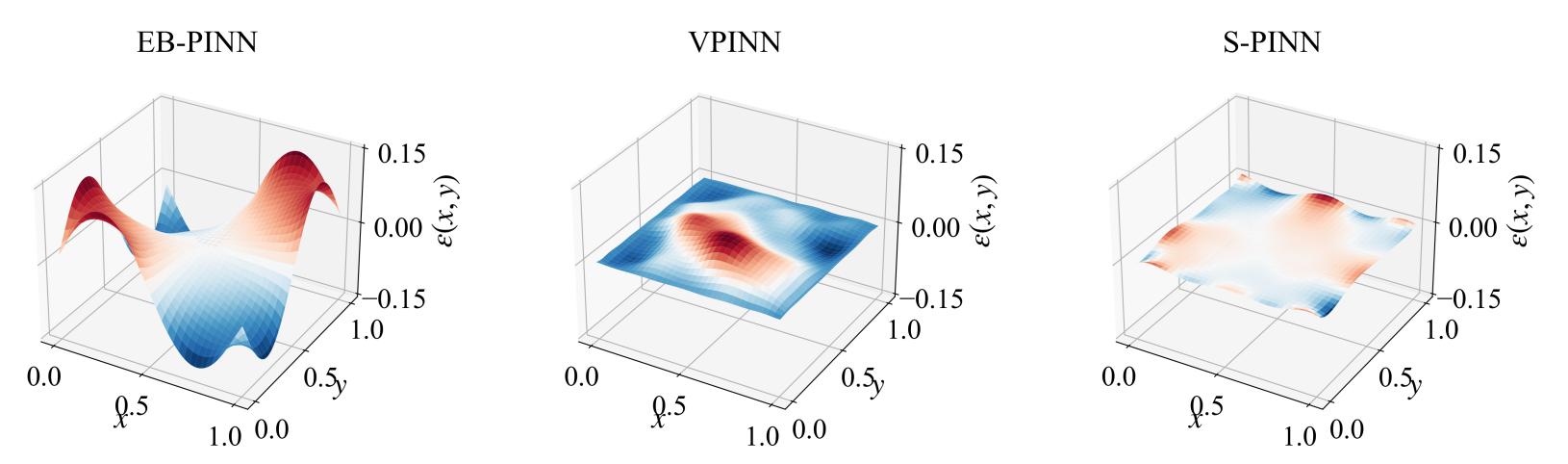
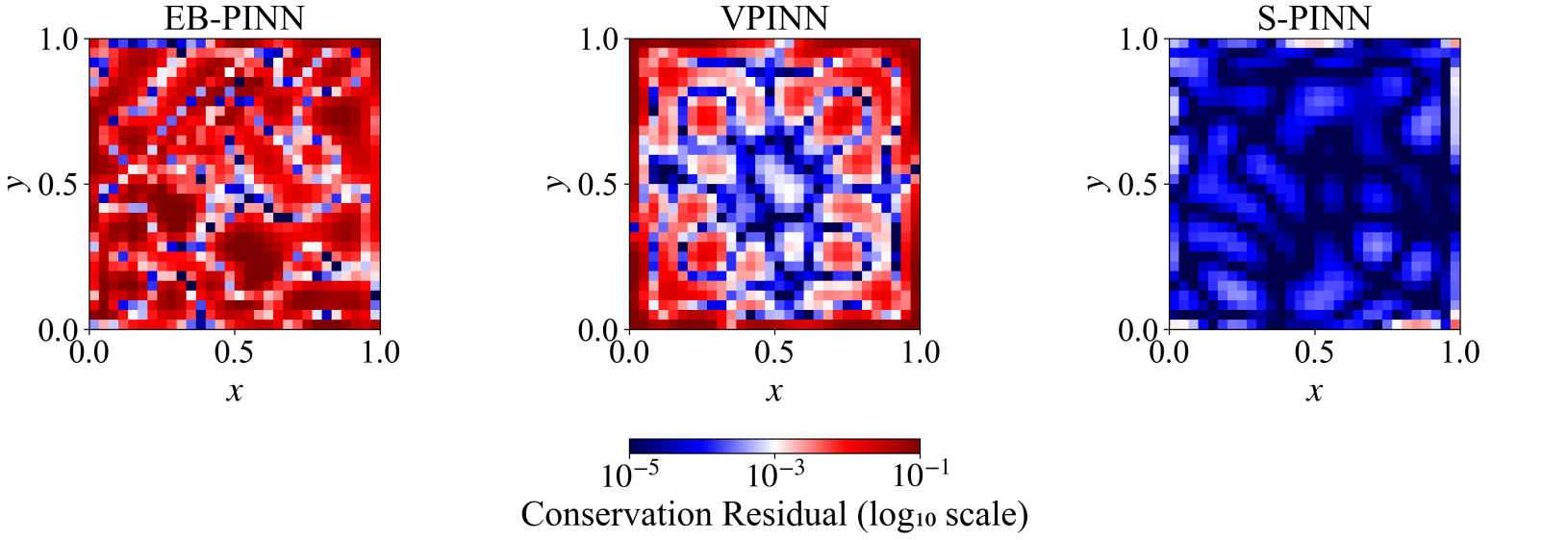
图3：泊松问题求解结果(第一行图)及其守恒性误差(第二行图), 其中EB-PINN为能量型PINN方法，VPINN为变分型PINN方法，S-PINN为该团队提出的新型稳定化PINN方法

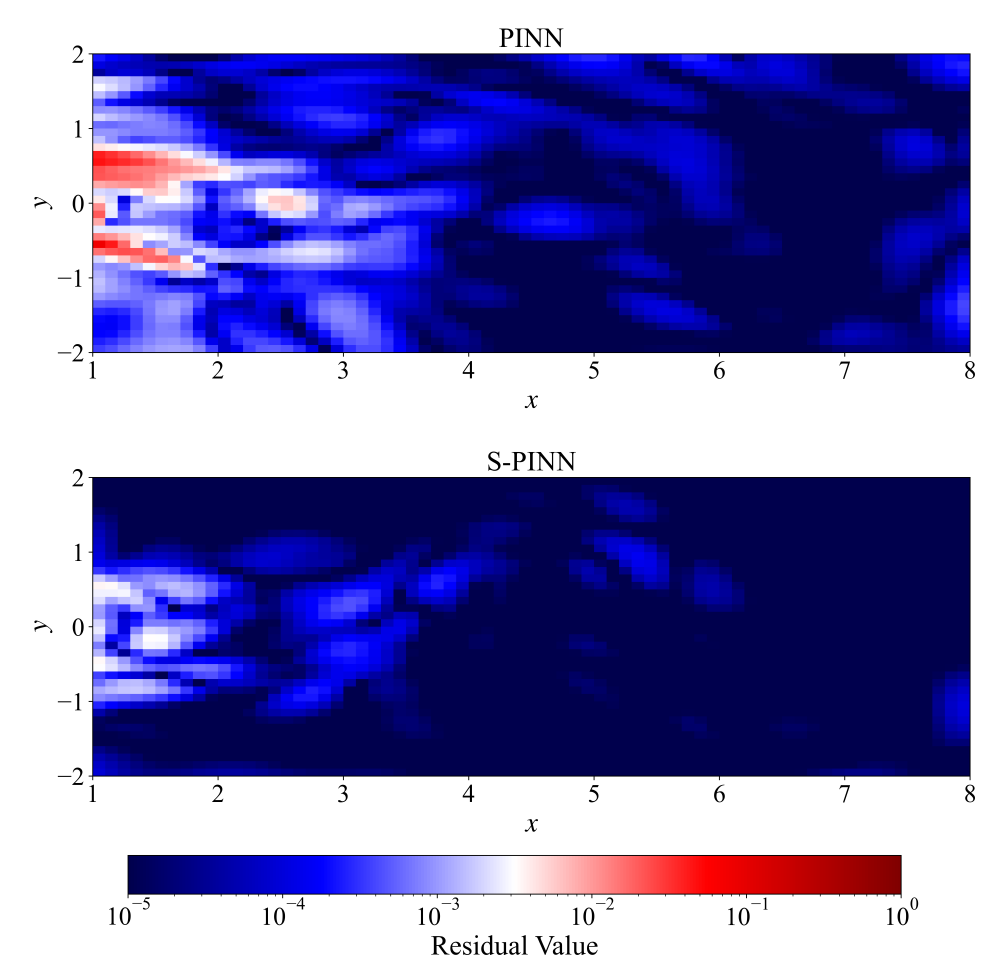
图 4：PINN与S-PINN在圆柱绕流问题中的守恒性误差分布

刘谋斌教授团队长期致力于复杂环境下多场耦合智能仿真算法与自主软件研发，发表SCI论文180多篇，Google学术引用16500多次。在SPH等无网格粒子方法、数智融合关键技术与工程应用方面取得系列原创成果，所开发的多场耦合数智算法与软件已经成功应用于海洋工程、防护工程及智能制造等众多领域。

钱志浩副研究员聚焦于高精度无网格粒子法、多物理场耦合仿真与智能计算方法等领域持续开展研究，相关成果发表于Computer Methods in Applied Mechanics and Engineering、Journal of Computational Physics和Applied Mathematical Modelling等国际顶级期刊，主持和参与多项国家自然科学基金、173项目和国家级实验室重点项目等。

该研究获国家自然科学基金和崂山国家实验室科技创新项目资助。北京大学力学与工程科学学院硕士研究生杨腾茂为论文第一作者，刘谋斌教授和钱志浩副研究员为共同通讯作者。

论文信息：

Tengmao Yang, Zhihao Qian*, Nianzhi Hang, Moubin Liu*, S-PINN: Stabilized physics-informed neural networks for alleviating barriers between multi-level co-optimization,Computer Methods in Applied Mechanics and Engineering 447: 118348, 2025.

论文链接：https://www.sciencedirect.com/science/article/abs/pii/S0045782525006206